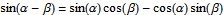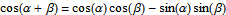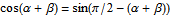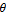Top 20 Posts for 2011

It's year end again. This year, I together with other guest bloggers  have created more than 100 applets this year.  The top 20 posts are shown below.

1. Circle Approximation Graph
2. Embedding GeoGebra Applets in Wordpress
3. The Pantograph
4. Approximating Pi
5. GeoGebra 4.0 release candidate and GeoGebra 4.2
6. Approximating the area of a circle
7. Graphing Piecewise Function
8. Triangle Angle Sum Proof
9. Centroid of a Triangle
10. Circumcircle of a Triangle
11. Graphs and Their Properties
12. Ferris Wheel
13. The Dancing Triangle
14. Pythagorean Theorem
15. Triangles and Quadrilaterals
16. Paper Folding and Proof
17. Visualizing Multiplication of Fractions
18. Folding a Hyperbola
19. Tracing the Ellipse
20. Viviani's Theorem

If you want to become a contributor of this blog, just email me at mathandmultimedia@gmail.com. You may also want to visit my two other blogs - Math and Multimedia and School of Freebies. 

Have a happy new year to all. 

Sine Difference Formula and Cosine Addition Formula

This applet shows a proof of the difference formula for sine,  and a proof of the addition formula for cosine,  using the formula .

This is a Java Applet created using GeoGebra from www.geogebra.org - it looks like you don't have Java installed, please go to www.java.com

Reference:

Proof of the Difference Formula for Sine and of the Addition Formula for Cosine" from the Wolfram Demonstrations Project
 http://demonstrations.wolfram.com/ProofOfTheDifferenceFormulaForSineAndOfTheAdditionFormulaFor/

Contributed by: Izidor Hafner

Minimum Area

Move the slider and observe the graph. 

This is a Java Applet created using GeoGebra from www.geogebra.org - it looks like you don't have Java installed, please go to www.java.com

The figure shows a semicircle of radius one and a horizontal line parallel to the diameter. What central angle corresponds to the minimum shaded area? This problem can be solved by either integration or trigonometry. The shaded area is equal to , where  is the central angle. The minimum shaded area occurs when the central angle is .


Download GGB File


Source:

 Abraham Gadalla

"Minimum Area between a Semicircle and a Rectangle"
 http://demonstrations.wolfram.com/MinimumAreaBetweenASemicircleAndARectangle/
 Wolfram Demonstrations Project
 Published: July 1, 2011

Java having trouble again?

I'm not really sure but for some reason GeoGebra Central does not load in two computers that I'm using. I wanted to post since last week, but I can't preview the applets. I'll see if I can post tomorrow using another computer.

Happy holidays everyone. 

Constructing triangles given the side lengths

Move AD, BE and CF to determine the side length of the triangle.

1 This is a Java Applet created using GeoGebra from www.geogebra.org - it looks like you don't have Java installed, please go to www.java.com

1.) Use the segment to construct the following triangles:
 a.) equilateral
 b.) scalene
 c.) isosceles
 d.) right

2.) Construct a triangle with side lengths 2, 2, and 4. What do you observe?
3.) Explain why your observations are such.

Download GGB file

The Parabola in Vertex Form

1. Move sliders a, h, and k. What do you observe? 
2. How are a, h, and k relates to the graph's movement? 
3. Make a generalization about the relationship between the parameters a, h, and k and the movement of the appearance of the graph.

This is a Java Applet created using GeoGebra from www.geogebra.org - it looks like you don't have Java installed, please go to www.java.com

The parabola has vertex form .

Download GGB File

You can now Like GeoGebra Applet Central on Facebook

You can now like GeoGebra Applet Central on Facebook. You can use the box below or the box  is located at the upper right part of the page.





You can also follow GAC on Twitter and Friendfeed. You can also subscribe to GACs Feedburner feeds. 

Rectangle-Triangle Area Relationship

Consider the rectangle and the triangle below.

1.  What do you observe? What are common properties between the two polygons?
2. Drag point D to change the height of the triangle and drag point A or B to change the length of the base. What do you observe?
3. What can you say about the areas of the two figures? Justify your answer. 
4. Click the Show Areas check box in the applet.  Was your answer in 3 correct? 
5. Drag point E. What is the relationship between the area of the rectangle and the area of a triangle? Explain why this is so. 

This is a Java Applet created using GeoGebra from www.geogebra.org - it looks like you don't have Java installed, please go to www.java.com

The applet above demonstrates that the area of a triangle is half the area of a rectangle with the same base and height.

Download GGB file

The Parallel Postulate

In the figure below, AB and CD are parallel lines. EF is a transversal.

This is a Java Applet created using GeoGebra from www.geogebra.org - it looks like you don't have Java installed, please go to www.java.com

The parallel postulate states that given two parallel lines (on the same plane) and a transversal, their corresponding angles are congruent. Using this postulate as shown above, determine the measure of the other angles and record your observations. Make a conjecture about them.

Download GGB file

GeoGebra Graphics 2 and the Sine and Cosine Functions

Move the point on the circle in the left window (Graphics 1).

This is a Java Applet created using GeoGebra from www.geogebra.org - it looks like you don't have Java installed, please go to www.java.com

This applet demonstrates how to use Graphics 2 of GeoGebra. Graphics 1 shows the distances on the circle: distance traveled (a)  by a point about the circle from (1,0), it's distance from the x-axis (b), and its distance from the y-axis (c).

Graphics 2 shows the two points with coordinates (a,b) and (a,c). The traces of the points in Graphics 2 forms the graph of the sine function and the consine function from 0 to pi.


Download GGB file.

The Mean Proportion

Move point Q and observe what happens.

This is a Java Applet created using GeoGebra from www.geogebra.org - it looks like you don't have Java installed, please go to www.java.com

In the figure, PSR is a semi-circle and with PR as the diameter.  Given a rectangle with side QR, and a triangle PSR, a square is formed using its height. The  square has the same are as the rectangle.

Download GGB file here.

GeoGebra 4.0 Tutorials and more...

This is to inform everyone that I am currently updating my GeoGebra Tutorials in Mathematics and Multimedia. I have updated the following tutorials so that they are compatible to GeoGebra 4.0.

• Introduction to GeoGebra
• GeoGebra Essentials 1 – Locating the Triangle’s Centroid
• GeoGebra Essentials 2 – Constructing a Rectangle

I will be updating three or more tutorials this weekend. If you are new to GeoGebra, I have created more than 50 GeoGebra tutorials categorized as follows.

• GeoGebra Essentials Series (10 tutorials for beginners)
• GeoGebra Basic Geometric Construction Series (7 tutorials for beginners)
• GeoGebra Intermediate Series (30 tutorials for beginners and intermediate users)
• GeoGebra Advanced (10 tutorials for advanced users)
• GeoGebra 4.0 Sneak Peek (New!) – 10 posts about GeoGebra 4.0

Please share the tutorials to people who might be interested. 

Polygons and Tessellation

Move the slider and observe what happens.

This is a Java Applet created using GeoGebra from www.geogebra.org - it looks like you don't have Java installed, please go to www.java.com

1. Which of the regular polygons tessellate? Can you explain why they do?
2. As n increases can we can find a regular polygons that tessellate? 
• If yes, how many of them can be found? Are they finite?
• If no, what is the maximum number of side of a polygon that can tessellate? Why?
3. Make a conjecture about your observations above. 

Download GGB File

If you want to know more about tessellation, you may want to check out the following articles that I have written:

• Tessellation: The Mathematics of Tiling
• Regular Tessellations: Why only three of them?

van Aubel's Theorem

Squares are placed outwardly at each side of quadrilateral ABCD. The center of the squares on the opposite sides are connected with segments (PN and MO). Move points A, B, C and D and observe what happens. Make a conjecture about your observations.

This is a Java Applet created using GeoGebra from www.geogebra.org - it looks like you don't have Java installed, please go to www.java.com

Van Aubel's Theorem

Given an arbitrary planar quadrilateral, place a square outwardly on each side, and connect the centers of opposite squares. Then van Aubel's theorem states that the two lines are of equal length and cross at a right angle.

Click here to download GGB file.

GeoGebra 4.0 offline installer, now available

If your PC/Mac is not always connected to the internet, or you have a computer laboratory with no internet connection, you can now download the GeoGebra 4.0 offline installer.

GeoGebra 5.0 Beta is also in development. 

Area of a Trapezoid

Move point A to change the shape of the trapezoid.  Then move slider  to the extreme right to rotate the trapezoid.

This is a Java Applet created using GeoGebra from www.geogebra.org - it looks like you don't have Java installed, please go to www.java.com

1.) What kind of quadrilateral  is formed when  equals 180 degrees? Justify your answer.
2.) What is the relationship between the area of trapezoid ABCD and the area of the quadrilateral formed in 1?
3.) Using the quadrilateral formed in 1, find the area of the trapezoid. Hint: Use  and .


Download GGB File

Testing Post - Social Network Integration

Recently, GeoGebra Central's automatic feed to Facebook and Twitter stopped. I am currently troubleshooting so please ignore this post. 

GeoGebra 4.0 now available

This is a repost from Math and Multimedia, my main blog. 

The long awaited  GeoGebra 4.0 is now available online. The Webstart files and Applet Start can be are fully functional.  Hopefully the offline installers will be available soon.

Some of the new features according to the website (haven’t explored all of them yet) are the following:

• GeoGebraTube: easily share worksheets online (see “File” menu)
• User interface: drag & drop, style bar, perspectives, accessibility
• New tools: data analysis, chart dialog, probability calculator, function inspector
• Copy & Paste, two Graphics views
• Inequalities and implicit equations
• Improved text tool, better equation displaying
• Filling options with hatching and images
• Animation of points on lines, dynamic limits for sliders & axes
• Buttons, input boxes, scripting
• Export to animated GIF
• 50 languages

To know more about the other features, go to the GeoGebra 4.0 Release Notes and the updated GeoGebra Manual. The GeoGebra Prim, the version for younger students is also now available.

I will be revising my GeoGebra tutorials soon to make them compatible with the new version.