This applet shows the graphical represenentation of the sum of two vectors. In the graph, u and v are vectors, and w = u + v. BD is the translation of AC and CD is the translation of AB. AD represents the sum of the vectors.
Download GGB File
Tuesday, January 31, 2012
Friday, January 27, 2012
Math and Multimedia Carnival will be hosted here
The Mathematics and Multimedia Carnival is on its 20th edition and will be hosted here. If you have a blog post about school mathematics, mathematics teaching and learning, multimedia tools, or any related article, you may submit here or email me directly at mathandmultimedia@gmail.com. The deadline of submissions is on February 18, 2012 and the post date is on February 20.
You may want to visit the following recent math carnivals:
- last month's edition of the Math and Multimedia Carnival
- Math Teachers at Play 46
- Carnival of Mathematics 85
To those who do not know what a carnival is, I have written a carnival primer in Math and Multimedia.
Wednesday, January 25, 2012
Deriving the Equation of the Parabola
Instructions: Move point A to adjust the position of the vertical line and move F along the x-axis as desired. Move C along the line and observe what happens.
Questions
1. What can you say about line a in relation to C and F?
2. Make a conjecture about segments PC and PF.
3.) Suppose P has coordinates (x,y), F has coordinates (2,0), and line d has equation x = 2, write the equation that would describe your conjecture in 2.
4.) Generalize the equation in 3 by changing the coordinates of F to (a,0) and line d has equation x = -d. Find the value of y.
Download GGB file
Questions
1. What can you say about line a in relation to C and F?
2. Make a conjecture about segments PC and PF.
3.) Suppose P has coordinates (x,y), F has coordinates (2,0), and line d has equation x = 2, write the equation that would describe your conjecture in 2.
4.) Generalize the equation in 3 by changing the coordinates of F to (a,0) and line d has equation x = -d. Find the value of y.
Download GGB file
Friday, January 20, 2012
Tangram Puzzle: Constructing a Square
Move the tangrams to construct a square. Drag the interior to change their position and use the 'blue point' on the vertex to rotate.
Download GGB File
Download GGB File
Tuesday, January 17, 2012
Squaring a Convex Polygon
This applet constructs a triangle with an area equal to the area of any convex polygon ABCDEF. The applet Squaring a Triangle shows how any triangle can be transformed to a square with an equal area. The combination of these two constructions shows how to square any convex polygon.
- Click on point F.
- Drag F to the right as far as it can go.
- Repeat these two steps three times, until the triangle is constructed.
Download GGB File
Monday, January 16, 2012
Squaring a Triangle
This applet shows the construction of a square with the same area as a given triangle.
Author: Irina Boyadzhiev of Ohio State University.
Download GGB File
Author: Irina Boyadzhiev of Ohio State University.
Download GGB File
Monday, January 9, 2012
Area of Triangles Under a Curve
Given: Right triangle BCD whose hypotenuse is tangent to the function f(x) = a/x.
- Move slider a and observe what happens? How is the appearance of the graph relate to a?
- Move point A and observe the triangle? What do you observe?
- What conjecture can you make based on your observation in 2. Prove your conjecture.
Thursday, January 5, 2012
Equation of a Circle
Move sliders h, k, and r to form the desired circle.
This applet shows that a circle can be determined given a center (h,k) and a radius r.
Download GGB File
This applet shows that a circle can be determined given a center (h,k) and a radius r.
Download GGB File
Monday, January 2, 2012
Routh's Theorem
Move ABC to determine the shape of a desired triangle and move the slider. What do you observe?
The Routh's theorem determines the ratio of areas between a given triangle and a triangle formed by the intersection of three cevians. The theorem states that if in triangle ABC points D, E, and F lie on segments BC, CA, and AB, then writing 
= x, 
= y, and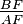 
= z, the signed area of the triangle formed by the cevians AD, BE, and CF is the area of triangle ABC times
= x, = y, and 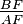= z, the signed area of the triangle formed by the cevians AD, BE, and CF is the area of triangle ABC times
This theorem was given by Edward John Routh on page 82 of his Treatise on Analytical Statics with Numerous Examples in 1896.
Source: Wikipedia
Download GGB file
Source: Wikipedia
Download GGB file
Subscribe to:
Posts (Atom)