Move ABC to determine the shape of a desired triangle and move the slider. What do you observe?
The Routh's theorem determines the ratio of areas between a given triangle and a triangle formed by the intersection of three cevians. The theorem states that if in triangle ABC points D, E, and F lie on segments BC, CA, and AB, then writing 
= x, 
= y, and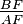 
= z, the signed area of the triangle formed by the cevians AD, BE, and CF is the area of triangle ABC times
= x, = y, and 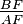= z, the signed area of the triangle formed by the cevians AD, BE, and CF is the area of triangle ABC times
This theorem was given by Edward John Routh on page 82 of his Treatise on Analytical Statics with Numerous Examples in 1896.
Source: Wikipedia
Download GGB file
Source: Wikipedia
Download GGB file
No comments:
Post a Comment